A clash of RL algorithms
Recently, my mentors and I just had a fruitful discussion on the various types of RL algorithms out there, namely DQN and PPO. And in this blog post, I thought I’d share what we talked about and what I’ve learned. So DQN, or deep-Q network, is a model-free RL algorithm that learns through Q-learning and off-policy. Two posts ago, I talked about what a policy was. If you recall, it’s basically the RL agent’s brain. Now, DQN and Q-learning in general are performed off-policy, meaning that while learning, each update in the policy can use data collected at any point in its time of training, whereas algorithms like PPO are on-policy, only using the data collected from the most up-to-date policy and making decisions based on that. Both algorithms are model-free, meaning that while training agents, they do not have access to the model of the environment. The model of the environment is a function which predicts state transitions and rewards. Here’s a neat little image taken from OpenAI Spinning Up’s course that gives a rough taxonomy of RL algorithms.
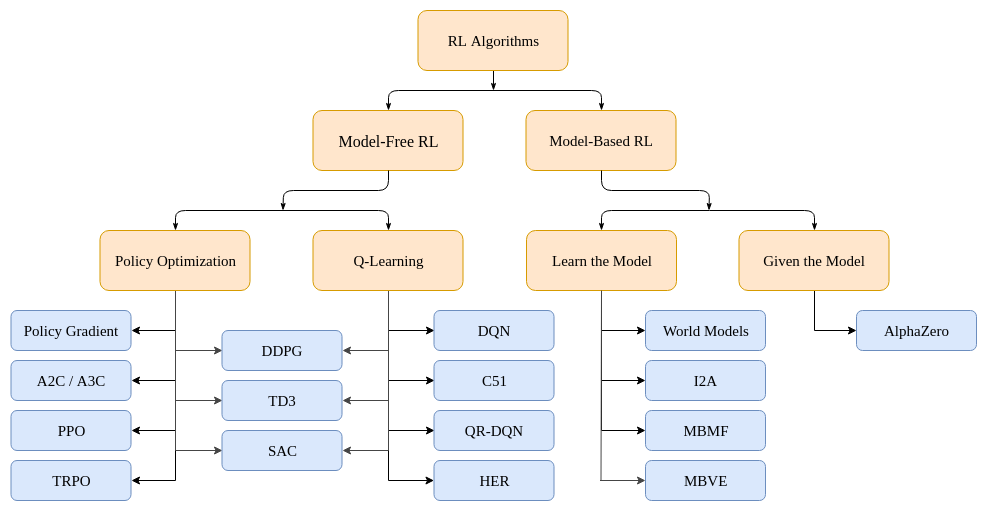
As you can see, both DQN and PPO fall under the branch of model-free, but where DQN and PPO differ is how they maximize performance. Like I said, DQN utilizes Q-learning, while PPO undergoes direct policy optimization. I already talked about PPO in a earlier blog post so for this one I’ll be focusing more on DQN and my experiences with it.
Q-learning
The backbone of the DQN algorithm is Q-learning. In Q-learning, the algorithm tries to learn a Q-function, which takes the state and action as inputs and returns the reward. We want to find a policy that will maximize the expected rewards and future rewards at any given state and taking some action. Mathematically, we want to find the optimal Q Function, $Q^*(s,a)$, which gives the expected return if you start in state $s$, take an arbitrary action $a$, and then forever after act according to the optimal policy, $\pi$, in a trajectory, $\tau$, of the environment:
\[Q^*(s,a) = max_{\pi} \mathbb{E}[R(\tau) | s_0 = s, a_0 = a]\]It’s clear then that the best action will be the maxium of the Q-function at a given state! If you recall, this is slightly different from PPO and policiy optimization. In PPO, recall that the only input is the state and the output is a probability distribution of all the actions. In Q-learning, we are implicitly learning a policy by greedily finding the action that maximizes the Q value.
But how do we learn such a magical Q-function?
Using deep neural networks! In DQN, the algorithm tries to approximate the Q-function using neural networks. In the case of Minecraft, the inputs to the neural network would be the pixels of each individual frame of Minecraft. Once we approximate a Q-function, the DQN algorithm then outputs a function that returns the action that gives the maxium reward in a given state. Pretty cool! There is a big problem though that I encountered. DQN does not work on continous action and observation spaces (action and observation spaces are continuous if there is a large range of possible values for an action. For example, turning a steering wheel. You can’t just say turn it left or right. A better way of saying it would be turn it x degrees to the left or right. But then the space becomes contiuous and the x degrees could be any continuous value. In Minecraft, turning your camera is obviously a continuous action space as you can move it anywhere and by any amount.) Only discrete ones (think Minecraft attacks. You either attack or you don’t attack. That’s a discrete action space.) Why? It becomes very hard to maximize a continuous function as the number of possible actions increase.
So in the case, using PPO was the much better choice as it pairs with continuous action spaces since you are not approximating a function but rather sampling from a probability distribution. But that isn’t to day DQN isn’t a good algorithm. DQN is a a classic that can be used in a decent amount of RL problems and also substantially launched the field of deep RL. Take a look at the official paper for a more dense, in-depth read. But that’s about it for this post. My experiences with both algorithms however provided a great learning experience for the types of algorithms out there in the world of RL. And being able to actually implement one for my purposes is definitely a huge success for me.